ریکٹانگل اور رومبوس کے درمیان فرق: ریکٹانگل بمقابلہ Rhombus

ریکٹانگل بمقابلہ Rhombus

روبوبس اور آئتاکار کواڈریٹرٹرالز ہیں. ان اعداد و شمار کی جامیات ہزاروں سالوں سے انسان کو جانتا تھا. یہ مضمون یونانی ریاضی دانش ایکلکڈ کی طرف سے لکھا "کتاب" عناصر میں واضح طور پر علاج کیا جاتا ہے.

Parallelogram

Parallelogram کے چار اطراف کے ساتھ جامیاتی اعداد و شمار کے طور پر تعریف کی جاسکتی ہے، اس کے برعکس ایک دوسرے کے ساتھ متوازی پہلوؤں کے ساتھ. زیادہ واضح طور پر یہ متوازی اطراف کے دو جوڑوں کے ساتھ ایک چوک ہے. یہ متوازی فطرت متعدد جغرافیائی خصوصیات کو متوازی کے ساتھ فراہم کرتا ہے.

مندرجہ بالا مندرجہ ذیل جیومیٹک خصوصیات ملنے کے لئے ایک چوکراہٹ ایک متوازی علامت ہے.

• مخالفت کے دو جوڑوں لمبائی میں برابر ہیں. (AB = DC، AD = BC)

• مخالفت کے زاویہ کے دو جوڑے سائز میں برابر ہیں. (

)

• قریبی زاویہ ضمیمہ ہیں

• ایک جوڑی جس کے ایک دوسرے کے مخالف ہیں، متوازی اور لمبائی برابر ہے. (AB = DC اور ABDDC)

• ڈریگن ایک دوسرے کو بیزار کرتے ہیں (AO = OC، BO = OD)

• ہر ڈریگنالے دو متعدد مثلث مثلثوں میں تقسیم ہوتے ہیں. (ΔADB ≡ ΔBCD، ΔABC ≡ ΔADC)

اس کے علاوہ، اطراف کے چوکوں کا اختتام ڈریگنوں کے چوکوں کے برابر ہے. یہ کبھی کبھی متوازی الحرمین قانون کے طور پر کہا جاتا ہے اور طبیعیات اور انجینئرنگ میں بڑے پیمانے پر ایپلی کیشنز ہیں. (AB ² + BC ² + CD ² + ڈی اے ² = AC ² + BD ² )

مندرجہ ذیل خصوصیات میں سے ہر ایک خصوصیات کے طور پر استعمال کیا جاسکتا ہے، ایک بار جب یہ قائم ہوتا ہے کہ چوتھا پاراہٹ ایک متوازی علامت ہے.

متوازی الحمام کے علاقے کی طرف سے ایک طرف کی لمبائی کی لمبائی اور مخالف طرف کی اونچائی کی طرف سے حساب کیا جا سکتا ہے. لہذا، متوازی لاگت کے علاقے کے طور پر کہا جا سکتا ہے

متوازی الحرمہ کے علاقے = بیس × اونچائی = AB × h

متوازی الحرمہ کے علاقے انفرادی متوازی علامت کے شکل سے آزاد ہے. یہ صرف بیس اور لمبی لمبائی پر منحصر ہے.

اگر ایک متوازی علامت کے اطراف دو ویکٹروں کی طرف سے نمائندگی کی جاسکتی ہے، تو اس علاقے کو دو ملحق ویکٹر کے ویکٹر کی مصنوعات (کراس کی مصنوعات) کی شدت کی طرف سے حاصل کیا جاسکتا ہے.

اگر اطراف AB اور AD باقاعدہ طور پر ویکٹر (

) اور (

) کی طرف سے نمائندگی کی جاتی ہیں، متوازی الحرم کے علاقے کی طرف سے دیا جاتا ہے، جہاں α

اور کے درمیان زاویہ ہے. >.

مندرجہ ذیل کچھ متوازی لاگت کے اعلی درجے کی خصوصیات ہیں؛

• متوازی الحمام کے علاقے میں سے کسی ایک کی مثلث کی طرف سے پیدا ایک مثلث کا علاقہ دو بار ہے.

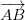
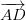
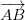
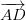
• متوازی لاگت کا علاقہ نصف پوائنٹ سے نصف میں تقسیم ہوتا ہے.

• کسی بھی عدم پسماندہ اثر میں تبدیلی کسی دوسرے متوازی لاگت پر متوازی علامت نہیں ہے

• ایک متوازی لاگت آرڈر 2 کی گھمائیی سمتری ہے

• کسی بھی اندرونی پوائنٹ کے کسی بھی نقطۂٔ نقطۂٔٔٔٔٔٔٔٔٔٔٔات سے قطع نظر اطراف سے آزاد ہے. نقطۂ جگہ کا مقام

مستطیل

چار دائیں زاویوں کے ساتھ ایک چوکاسٹک آئتاکار کے طور پر جانا جاتا ہے. یہ متوازی علامت کا ایک خاص معاملہ ہے جہاں کسی بھی دو قریبی اطراف کے درمیان زاویہ صحیح زاویہ ہیں.

ایک متوازی لاگت کے تمام خصوصیات کے علاوہ، آئتاکار کی جیٹریری پر غور کرتے وقت اضافی خصوصیات کو تسلیم کیا جا سکتا ہے.

• عمودی میں ہر زاویہ صحیح زاویہ ہے.

• ڈریگن لمبائی میں برابر ہیں، اور وہ ایک دوسرے کو بیزار کرتے ہیں. لہذا، bisected حصوں لمبائی میں بھی برابر ہے.

• ڈریگنلز کی لمبائی پائیگراوراس 'پریمیم کا استعمال کرتے ہوئے کی جا سکتی ہے:

PQ

2

+ PS ² = SQ ² • علاقے فارمولہ لمبائی اور چوڑائی کی مصنوعات کو کم کر دیتا ہے. ^{آئتاکار = لمبائی × چوڑائی}

علاقے میں • آئتاکار خصوصیات میں بہت سارے سمیٹ کی خصوصیات ملتے ہیں؛

- ایک آئتاکار سائیکل ہے، جہاں تمام عمودی طور پر ایک دائرے کے فریم پر رکھا جا سکتا ہے.

- یہ متغیر ہے، جہاں تمام زاویہ برابر ہے.

- یہ واحد ہے، جہاں تمام کونوں میں اسی سمتری مدار کے اندر اندر جھوٹ ہے.

- اس میں عدم اطمینان اور گردش دونوں سمتری ہے.

رومبوس

تمام پہلوؤں کے ساتھ ایک چوڑائی برابر لمبائی میں برابر ہے جو ایک قبروم کے نام سے جانا جاتا ہے. یہ ایک

متوازن چوکیدار

کے طور پر بھی نامزد کیا جاتا ہے. اس کے کھیل ہی کھیل میں ایک ہی طرح کی ایک ہیرا شکل سمجھا جاتا ہے. رومبوس بھی متوازی علامت کے ایک خصوصی کیس ہے. یہ برابر چاروں طرف برابر متوازی علامت کے طور پر سمجھا جا سکتا ہے. اور اس میں متوازی لاگت کی خصوصیات کے علاوہ، خصوصی خصوصیات مندرجہ ذیل ہیں. • روبوس کی وینگالیں ایک دوسرے کو صحیح زاویہ پر بیزار کرتی ہیں؛ ڈریگن پورٹیولک ہیں.

• ڈرنجنس دو مخالف اندرونی زاویہوں کو چھوڑے ہیں.

• کم سے کم دو کے قریب اطراف لمبائی میں برابر ہیں.

تالب کا علاقہ اسی طرح میں متوازی کے طور پر شمار کیا جا سکتا ہے.

روبوس اور آئتاکار کے درمیان کیا فرق ہے؟

• روبوبس اور آئتاکار کواڈریٹرٹرلز ہیں. مستطیل اور مقبوضہ متوازی انباروں کے خصوصی معاملات ہیں.

• کسی بھی علاقے میں فارمولا

بیس × اونچائی

کا استعمال کرتے ہوئے شمار کیا جا سکتا ہے. • ڈرنگنز پر غور کرنا؛ - روبوس کا ڈریگن ایک دوسرے کو صحیح زاویہ پر بیزھا کرتی ہے، اور مثلث مثلث برابر ہے.

- آئتاکار کے ڈرنگ لمبائی میں برابر ہوتے ہیں اور ایک دوسرے کو بیزار کرتے ہیں؛ bisected حصوں لمبائی کے برابر ہیں. ڈرنگنز آئتاکاروں کو باہمی باہمی مثلثوں میں بکس لگاتے ہیں.

• اندرونی زاویہ پر غور؛

- روبوس کے اندرونی زاویہ وینکلز کی طرف سے bisected ہیں

- آئتاکار کے چار اندرونی زاویہ صحیح زاویہ ہیں.

• اطراف پر غور کرو؛

- جیسا کہ چار چار پہاڑوں میں ایک مقبوضہ ہیں، چار دفعہ ایک طرف چار چوڑائی ڈرنگنل کے چوکوں کے برابر ہے (پیرامیگلرام قانون کا استعمال کرتے ہوئے)

- آئتاکاروں میں، چوکوں کی رقم دو قریبی اطراف کے اختتام کے اختتام کے اختتام کے برابر ہے.(پائیگراوراس کے اصول)