فرق اور غیر انتفاعی انضمام کے درمیان فرق
کیلکولیشن ریاضی کے ایک اہم شاخ ہے، اور تنازع کیلوری میں اہم کردار ادا کرتا ہے. علیحدگی کا انفرادی عمل انضمام کے طور پر جانا جاتا ہے، اور انواسطہ طور پر جانا جانا جاتا ہے، یا صرف ڈال دیا جاتا ہے، انفرادی طور پر انفرادی طور پر ایک لازمی دیتا ہے. نتائج کے مطابق وہ انضمام پیدا کرتے ہیں دو کلاسوں میں تقسیم ہوتے ہیں. ، درست اور غیر واضح مطابقت.
واضح انٹیگریٹڈ
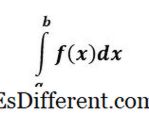
ایک مخصوص نمبر f (x) ہے اور اس علاقے کے وکر f (x) x = a سے ایکس = بی . ایک قطعی طور پر لازمی طور پر انضمام پر اوپری اور کم حدود موجود ہیں، اور اس کا معنی یہ ہے کہ اس مسئلے کے خاتمے میں، ہمارے پاس ایک نمبر ہے - یہ ایک درست جواب ہے.
f (x) کی غیر معتبر انضمام ایک فنکشن ہے اور سوال کا جواب دیتا ہے، "مختلف فعل جب مختلف ہوتی ہے

f (x) ؟ " یہاں غیر لازمی طور پر انضمام کے ساتھ یہاں تک کہ انضمام پر اوپری اور کم حدود موجود نہیں ہیں، اور جو کچھ ہم ملیں گے اس کا ایک جواب یہ ہے کہ اب بھی اس میں ایکس
ہے اور اس میں بھی مسلسل (عام طور پر C کی طرف سے منظور کیا جاتا ہے).
F
کی تفریق کی دوسری تقریب
f کی طرف جاتا ہے، اور F کے انضمام کو لازمی دیتا ہے. علامتی طور پر، اس کے طور پر لکھا جاتا ہے F (x) = ∫ƒ (x) dx یا F = ∫ƒ dx
جہاں دونوں
F
اور
ƒ < کام کرتا ہے x ، اور F مختلف ہے. مندرجہ بالا شکل میں، یہ ایک Reimann انضمام کہا جاتا ہے اور نتیجے کی تقریب ایک مباحثہ مسلسل ساتھ ساتھ. ایک غیر معتبر انضمام اکثر افعال کے ایک خاندان پیدا کرتا ہے؛ لہذا، انضمام غیر یقینی ہے. انضمام اور انضمام کے عمل متفرق مساوات کو حل کرنے کے دل میں ہیں. تاہم، مختلف حالتوں کے برعکس، انضمام میں قدم ہمیشہ واضح اور معیاری معمول کی پیروی نہیں کرتے. کبھی کبھار، ہم دیکھتے ہیں کہ ابتدائی طور پر حل ابتدائی طور پر ظاہر نہیں کیا جا سکتا. اس صورت میں، تجزیاتی حل اکثر غیر لازمی طور پر لازمی طور پر دیا جاتا ہے. کیلکولیشن کا بنیادی نظریہ خاص اور غیر معتبر انضمام کیلکولیٹس کے بنیادی نظریہ کی طرف سے منسلک ہوتے ہیں جیسا کہ:
قطعی طور پر لازمی
کو مرتب کرنے کے لئے،
غیر معتبر اجتماعی کو تلاش کریں <(99) x = a
اور x = b اختتام پر کے فعل کے طور پر (جس میں اینٹی ڈیوکیٹ کے طور پر بھی جانا جاتا ہے) بھی. ایک مخصوص تقریب کے لئے ضم کے ایک بار کے بعد مقررہ اور غیر واضح مطابقت کے درمیان فرق واضح ہو جائے گا. مندرجہ بالا لازمی طور پر غور کریں: ٹھیک ہے. دو کرتے ہیں اور فرق کو دیکھتے ہیں. انضمام کے لئے، ہمیں ایک انڈیکس میں شامل کرنے کی ضرورت ہے جو ہمیں مندرجہ ذیل بیان میں لیتا ہے: اس وقت سی صرف ہمارے لئے مستقل ہے.
C
کی عین مطابق قیمت کا تعین کرنے کے لئے مسئلہ میں اضافی معلومات کی ضرورت ہے.

ہم اس کے مخصوص فارم میں اسی انٹرویو کا اندازہ کریں. ای. ، اوپری اور کم حدود کے ساتھ شامل تھے.
گرافیک بول رہا ہے، ہم اب علاقے میں f (x) = y
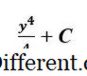
3 y = 2 اور y = 3 >.
اس تشخیص میں پہلا مرحلہ یہ ہے کہ انفرادی طور پر لازمی تشخیص. فرق یہ ہے کہ اس وقت ہم اس وقت مسلسل نہیں ہیں

سی . اس معاملے میں اظہار مندرجہ ذیل طور پر نظر آتا ہے: یہ بدل جاتا ہے: لازمی طور پر ہم نے اظہار میں 3 اور پھر 2 کو متبادل کیا اور ان کے درمیان فرق حاصل کیا. یہ ایک خاص قدر ہے جس کے مقابلے میں مسلسل سی کے استعمال کے مخالف ہے.
ہمیں کچھ اور تفصیل میں مستقل عنصر (غیر معتبر مطابقت کے بارے میں) کے بارے میں آگاہ کریں. اگر y
3


3y
2 ، ∫
3y
2 dy = y 3 تاہم، 3y 2 بہت سے اظہارات کے فرق ہو سکتا ہے جن میں سے کچھ میں شامل ہیں
y 3 -5 ، > y 3
+7 ، وغیرہ … اس کا یہ مطلب یہ ہوتا ہے کہ ریفرنڈیل منفرد نہیں ہے کیونکہ اس آپریشن کے دوران مستقل طور پر ناقابل یقین ہے. تو عام طور پر، 3y 2 فرق y 3 + سی کہاں سی کسی بھی مستقل ہے. واضح طور پر، سی
'انضمام کی مسلسل' کے طور پر جانا جاتا ہے. ہم اسے لکھتے ہیں: ∫ 3y 2 . dx = y 3 + سی ایک غیر معتبر انضمام کے لئے انضمام کی تکنیک، جیسے ٹیبل کی تلاش یا ریش انضمام، انضمام کے عمل کے دوران نئی رکاوٹ شامل کرسکتے ہیں. یہ نئے رکاوٹوں کو ظاہر ہوتا ہے کیونکہ اینٹی ذیابیطس پیچیدہ لارنٹریز کے تعارف کی ضرورت ہوتی ہے. کمپلیکس لارنرسمس کو چھلانگ کی رکاوٹ ہوتی ہے جب دلیل منفی اصلی محور کو پار کرتی ہے، اور انضمام الگورتھم کو کبھی کبھی ایسی نمائندگی نہیں مل سکتی جہاں یہ چھلانگ منسوخ ہوجاتی ہیں.
اگر مکمل طور پر لازمی طور پر انفرادی طور پر مطابقت پذیر ایک لازمی مطابقت پذیر ہو اور اس کے نتیجے میں انضمام کی حدوں کو تبدیل کرنے کی طرف سے اندازہ کیا جاسکتا ہے، تو ہمیں لازمی طور پر معلوم ہونا چاہئے کہ غیر معتبر انضمام کو روکنے کی صلاحیت پیدا ہوسکتی ہے. اگر یہ کرتا ہے، اس کے علاوہ، ہمیں انضمام وقفہ میں discontinuities کی تحقیقات لازمی ہے.




